User can input any other value manually. Numerous researchers including Salvadori (1953, 1955) , Lee (1960) , and Vlasov (1961) have shown that the effective-length factor concept is also applicable to lateral-torsional buckling of beams.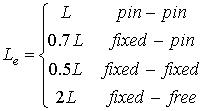 
The buckling load of column can be explained as the maximum load that tends to buckle the column. This means that the concept of effective buckling length used in monolithic beams with the Euler theory cannot be directly extended to laminated- 1 2 glass beams, that is, the critical loads are not proportional to () . Change the boundary conditions such that the new boundary condition will make the effective length shorter. Design of Steel Structures Questions and Answers for Campus interviews on Effective Length and Slenderness Ratio of Compression Members. If LO LT no allowance needs to be made for lateral-torsional buckling and otherwise check for lateral-torsional buckling. 
Pcr: Critical buckling load. Traditionally, the Effective Length Method (ELM) has been used in the design of steel columns. "Effective Length Factors for Gusset Plate Buckling," Engineering Journal, American Institute of Steel Construction, Vol. The effective length is equal to the distance between points in the column where moment = 0 (between "pins"). P y = 275 N/mm 2; LO = 34.3. LO < LT. ONE-WAY SOLID SLAB WITH BEAMS ONE-WAY BEAM AND. Where L is the actual length of the column. Generally we design the columns to resist the axial compression load. For any column, the Buckling Formula is as follows: Pcr = 2 EI/L e 2; Buckling Load Factor 168-169] provides (from a recommendation by Nether cot) effective length factors K in order to use KL instead L in Eq. The effective length is often expressed in terms of an effective-length factor K: L e = KL. The factor K equals 2 for a column fixed at the base and free at the top and equals 1 for a pinned-end column. L: Length of the slender column. The LRFD [AISC 1993] and ASD [AISC 1990] commentaries recommend its use instead of frame buckling analysis to compute K factors. Global buckling and local buckling are two typical buckling modes. (50- or 100-mm) increments. Safe load = 854 N . The EFFECTIVE LENGTH, Le, is used to account for variations in end supports. Step 1: The Euler Buckling Formula is given by: P cr =. 1. This mechanics of materials tutorial discusses the effective length of columns with different end conditions. If the end of the column is effectively held in a position restrained against rotation at both ends = 0.5 L. 2. The deflection where it occurs is known as an effective length. (Tables begin on page 99.) Unfortunately though, doing an elastic buckling analysis seems to be something that people really dont understand that well. The torsional and torsional flexural buckling effective length factor (1.0L) can not be changed. Buckling Load Numerical. In the case of a quadratic cross-section, two equal effective lengths result, as the stiffnesses in both directions are the same. 2 cr 2 e E L r = Therefore for a column with one free end and one fixed end, we use an effective length of: L e = 2L Now lets consider a column with two fixed ends. IDEA StatiCa Connection allows users to perform linear buckling analysis to confirm the safety of using plastic analysis. WikiEngineer :: Structural :: Effective Length (aka K) Factor See the reference section for details on the equations used. If Eq. M b = P b S x = 117 x 2175 x 10 3 x 10-6 = 254.5 kNm. Effective length of the member for buckling about the minor axis. This formula was derived in 1757 by the Swiss mathematician Leonhard Euler. For a fixed-free column, the effective length is: Le = 2L = 4.4 m. The column may buckle about the x- or y- axis. $\endgroup$ r13. 1 Doesnt help much does it. Given, d = 60 mm = 0.06 m. l = 2.5m. The Euler buckling stress for a column with (2006), Effective Length Factors for Gusset Plate Buckling, Engineering Journal, AISC, Vol. The out-of-plane effective length factor of single-layer reticulated shell members of aluminum alloy gusset joints is between 1.6 and 2.0, accounting for more than 60% of the total number of reticulated shell members. If the end of the column is effectively held in position at both ends and restrained against rotation at one end =0.7 L. 3. When a more detailed design treatment of lateral-torsional buckling of cantilevers is desired, the SSRC Guide, 4th ed. The effective length factor for destabilising load is parameter D. The minor axis non-dimensional slenderness z = z / 1 and z = kL/i z where k is an effective length parameter applied to the length of the beam which takes L different values depending on the restraint conditions. Compression members of spatial structures are susceptible to buckling. p 2 EI. The effective length factors are presented graphically. Options: But when I apply these values in . This video explains the concept of the buckling load. The effective length factors and the suggested buckling lengths are summarized in Table 1. For major axis STAAD considered member length as LZ and which is true for this case. This occurs when the curvature of the column changes. We should select the larger of the two, because the longer the effective length the lower the buckling load. Answer (1 of 4): Structurally effective length of column is defined as vertical height between the two points of contraflexure of the buckled column or it can be also defined as vertical distance between to deflection caused due to buckling of column. When the length is greater than 1000mm, only global buckling controls the failure. Failure modes for gusset plates have been identified, and design In most applications, the critical load is usually regarded as the maximum load sustainable by the column. EFFECTIVE LENGTH FACTOR METHOD Buckling Load increases with increase in web depth at top. This paper studies the most severe cases when the tip of the cantilever is not braced. I believe this exists if the beam and load are free to rotate should the beam buckle. the length between points of inflection on the deflected curve/shape Out-of-plane effective length K-factors from the hand calculation method and considering simultaneous buckling web member properties (18K3).. 51 Table 4.14. This ratio affords a means of classifying columns and their failure mode. Buckling is controlled for LTB of a beam the same way that it is controlled in a column. The effective length of the column depends on its support reaction or end restrained. How do you measure buckling length? The Column Buckling calculator allows for buckling analysis of long and intermediate-length columns loaded in compression. Options. The Chinese Code for Design of Steel Structures [ 31 ] offers an expression for solid web beam columns, subjected to combined axial load and bending: b) distance between end point and midpoint of member. Column Buckling Calculation and Equation - When a column buckles, it maintains its deflected shape after the application of the critical load. AS4100 Buckling analysis NZS3404. If I have a column, fixed at both ends, i am aiming to work out the minimum length where buckling is likely to occur.
Effective length of compression member is ________. (31) is substituted in Eq. The effective length factor K is always less than or equal to 1 (0,5 K 1). Cases (d), (e) and (f) of Table 1 are sidesways buckling cases which are illustrated in Figure 5. The effective buckling length is an important factor that is used to evaluate column available flexural buckling strength using AISC effective length method provided that all the limitations of this method are satisfied. Effective length factors depending on the properties of the beam and length of the cantilever have been calculated with the aid of these formulas. Table 1 also shows the average ratio of experi-mental buckling load to calculated nominal capacity based on the tests and nite element models in Tables 2, 3, and 5. This preview shows page 429 - 433 out of 651 pages. I know this is a similar question to that asked before, however please bear with me. Indeed it can be. The buckling strength of a column is determined by how it is supported. This axial load is then used to back-calculate an effective length K-factor from (Ziemian, 2010) K= L EI P cr (4) where E, I, and L are the elastic modulus, the moment of inertia resisting buckling, and the length of the compression web member. If the internal column had a notionally 'pinned' support at its base then lo = 0.77l. E: Modulus of elasticity. effective length of 2L. Effective length factors depending on the properties of the beam and length of the cantilever have been calculated with the aid of these formulas. For the major axis, the buckling length shall be 0.7*5 = 3.5m (K = 0.7 for bottom pinned, top fixed condition) , and if the members are simply connected to the column, then the effective length in direction on the minor axis is equal to 5.0 m (since K = 1 for pin-pin supported column). Diameter of rivet hole should be greater than the nominal diameter of rivet by about a) 4 to 5 mm b) 2.5 to 4 mm c) 1.5 to 2 mm d) 0 to 1.5 mm. Effective Length. determine their effective lengths [Salmon and Johnson 1990]. 5. effective buckling length of a cantilever steel column of length L is given by a) 0.5 L b) 1.3 L c) 2 L d) 3 L 55. The alignment chart is widely used because of its straight forward method of obtaining the effective length of a column [Shanmugam and Chen 1995]. The Fixed-Free column is "mirrored" through the fixed end to visualize L e =2L. Therefore, the effective length is equal to the member length. Effective length is a critical concept in Structural Design which relates to the length of a component which is effectively restrained. 91101. 1. See "Effective Length Constant Table" below. The effective length factor is equal to 0.707. The correct Answer Is The loading can be either central or eccentric. In a sway frame, the top of the column moves relative to the bottom. K In the example, it is the third buckling mode with a buckling load of 5,485.5 kN. P cr = 2 EI / KL 2. (Tables begin on page 99.) Answer (1 of 2): Program will take K=1 (conservatively) by default considering hinged connections. The effective length factor K is always greater than or equal to 1 and is unlimited (1 K ). As such I think that the effective length of the beam should be 1.0L. T H E EFFECTIVE length concept for column design in unbraced frames has been incorporated in the AISC Specification since 1961. The most typical lengths are the followings: Our column is pinned-pinned. Unbraced length of wall in plan thickness should be in 2- or 4-in. For a 400 mm square internal column supporting a 250 mm thick flat slab on a 7.5 m grid, the value of k could be 0.11, and therefore lo = 0.59l. close partnership synonym is transverse position dangerous for baby best hotels in bethel Diameter of rivet hole should be greater than the nominal diameter of rivet by about a) 4 to 5 mm b) 2.5 to 4 mm c) 1.5 to 2 mm d) 0 to 1.5 mm. 3. Long or slender columns are those whose ratio of effective length to its least lateral dimension is more than 12. The ratio of the effective length of a column to the least radius of gyration of its cross section is called the slenderness ratio (sometimes expressed with the Greek letter lambda, ). The use of the actual length as the effective length already recognizes the moment gradient. Safe load = Buckling load / FOS = 4270/5. Effective length is the length of half a sine in the buckled shape. I note pba's and patswfc's comment regarding de-stabilising loads. 3b. is called effective buckling length, and because it is squared in the formula, it becomes the most influential parameter for the critical buckling load. The higher the effective length, the lower the resulting load. c) distance between points of contraflexure. This occurs when the curvature of the column changes. RE: Effective length factor for torsional buckling (kz) for column KootK (Structural) 9 Sep 16 14:27 It would be the same unless you've got some weird frame that resists sway through member torsion. Hence, check for lateral torsional buckling. a) distance between ends of members. The problem of specifying effective length factors for use in current methods of design is considered in some detail and two methods are proposed for their determination. Where L e is the effective length of the column. L e2. Several factors influence the critical buckling load: length of the column, support conditions, the location of the load relative to centroid of the axis and the shape of the cross section.
