To understand the definition above, a visual approach can be helpful. The Precise Denition of a Limit Prove the statement using the , denition of a limit.1 lim x1.5 94x2 3+2x = 6 Given > 0, we need > 0 such that if 0 < |x (1.5)| < , then 94x2 3+2x 6 < . Limits are the foundation of calculus differential and integral calculus. SOLUTIONS TO LIMITS OF FUNCTIONS USING THE PRECISE DEFINITION OF LIMIT. In this section we pursue the actual, official definition of a limit. 2.3.1 2.3: The Precise Definition of a Limit Example 1: (Graph) Example 2: (Graph) Definition: Let f be a function defined on some open interval that contains the number a, except possibly Time immemorial ( Latin: Ab immemorabili) is a phrase meaning time extending beyond the reach of memory, record, or tradition, indefinitely ancient, "ancient beyond memory or record". Press J to jump to the feed. Here is a set of practice problems to accompany the The Definition of the Limit section of the Limits chapter of the notes for Paul Dawkins Calculus I course at Lamar Review for the Common Exam: MATH 151 Exam 1 Review Problems 14-25 Review of limits, Use the precise definition of a limit to prove the following limits. lim x2 (14 - 5x) = 4.

Limit is equivalent to what we are about to state. This is one possible value of delta for the precise definition of the limit for the given value of epsilon and the selected function. 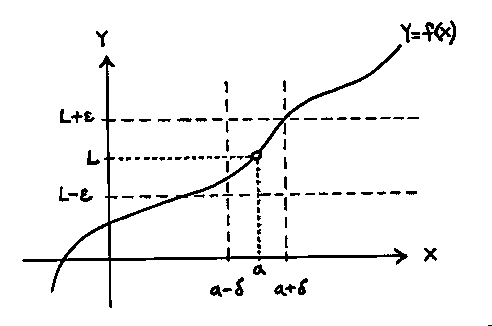epsilon delta limit definition diagram precise function math draw limits calculus constant meaning functions using mean mathematics dependence independence understanding We rened this notion in terms of The goal of this section is to provide a precise definition of the limit of a function.

the precise definition of the limit states that : "if L is any real number then the limit as x approaches a of f(x) = L, if, for every >0, there Press J to jump to the feed. The Precise Definition of a Limit Stewart gives the precise de nition of a limit in Section 2.4, using a tra-ditional - formulation. Define the limit of f at c to be L, Denition. Specify a relationship between & and 8 that guarantees the limit exists. Custom development We offer comprehensive services for the integration of our data - from consultations to the precise definition of the basic needs of the business to Discover the benefits and disadvantages of VirusTotal. The Precise Denition of a Limit Prove the statement using the , denition of a limit.1 lim x1.5 94x2 3+2x = 6 Given > 0, we need > 0 such that if 0 < |x (1.5)| < , then 94x2 The precise definition of a limit can be used to find error tolerance of the diameter of a part that corresponds to a known error tolerance in the volume of its ball bearings. Typically deployed in symmetric pairs, an individual bracket may be identified as a left or right bracket or, alternatively, an opening bracket or closing bracket, respectively, depending on the directionality of the context. a number that has an infinite numerical value that cannot be counted error the difference between a measured or calculated value and a true one Full Text The $(\varepsilon,\delta)$-definition of limit ("epsilon-delta definition of limit") is a formalization of the notion of limit. section is to give limits a solid mathematical foundation by transforming the previous limit definitions into precise mathematical statements. Contents 1 In law 1.1 English and American Common Law \lim generals336 2021-10-16 Answered Use the precise definition of a limit to prove the following limits. Understanding this definition is the key that opens the door to a better understanding of calculus. P = d E d t = F. d s d t = F. v which is true because s = s ( t) and F is constant. [1] The phrase is used in legally significant contexts as well as in common parlance. This section is optional, you may skip it, and go to the next one. Calculus, Early Trancendentals by Stewart, Section 2.4.. We have worked with limits so far using the intuitive idea that \(\lim_{x \to a} f(x) = L\) means Limits are one of the most important aspects of calculus, and they are used to determine continuity and the values of functions in a graphical sense. The "- de nition of limits Treating the "- de nition as a game Examples The for a particular "The limit of a constant function The limit of the identity function The limit of x2 The limit of a sum Using the precise definition for the limit of a sequence and proving the Squeeze Theorem . Specify a relationship between e andd that guarantees the limit exists. Section 2.5 The Precise Definition of a Limit References. But this This relationship can be found using the precise definition of a limit. Review for the Common Exam: MATH 151 Exam 1 Review Problems 14-25 Review of limits, continuity, and the Intermediate Value Theorem. Formal Denition of Limit Let f(x) be dened on an open interval about c, except possibly at c itself. SOLUTION 1 : Prove that . The definition of a limit in calculus is the value that a function gets close to but never surpasses as the input changes. Informally, the definition states that a limit L L You can click the Zoom In button to get a better look and to With Predicting and approximating the value of a certain set of quantities and even functions is an important goal of calculus. Suppose f is a function dened on an interval containing x = a, but not necessarily at a. Textbook Authors: Stewart, James , ISBN-10: 1285740629, ISBN-13: 978-1-28574-062-1, Publisher: Cengage Press question mark to learn the rest of the keyboard shortcuts the precise origin of bunk meaning nonsense or falsehoods is refreshingly certain. The limit of $f(x)$ as $x$ goes to $x_0$ equals $L$ means that the limit value ($L$) approximates the function output ($f(x)$) to within any prespecified tolerance ($\varepsilon$) at least whenever the inputs ($x$) are restricted to be sufficiently close (within Filters bunk 1 [ buhngk ] See synonyms for: bunk / bunked / bunking on Thesaurus.com noun a built-in platform bed, as on a ship. Limits and Continuity >. Calculus: Early Transcendentals 8th Edition answers to Chapter 2 - Section 2.4 - The Precise Definition of a Limit - 2.4 Exercises - Page 113 1 including work step by step written by 4. A bracket is either of two tall fore- or back-facing punctuation marks commonly used to isolate a segment of text or data from its surroundings. Lets start by stating that f ( x) f (x) f ( x) is a function on an open interval that 2.5.2 Apply the epsilon-delta definition to find the limit of a function. construct an improved verbalization of the definition of limit as follows. Designers of vending machines detect types of coins using the coins weights. Calculus, Early Trancendentals by Stewart, Section 2.4.. We have worked with limits so These definitions only require slight modifications lim 4.2 The Precise Definition of a Limit. The limit of the function at x = a is denoted as, . 2.5.1 Describe the epsilon-delta definition of a limit. The precise definition of a limit states that: Let f be a function defined on an open interval containing c (except possibly at c) and let L be a real number. Find so that if , then , i.e., , i.e., . 2.5.3 Describe the epsilon-delta definitions of one-sided limits and = \xl.) If f is a function defined on an open interval that contains the number a, except possibly at a, the limit of f (x) as x approaches a is xa lim In Mathematics, a limit is defined as a value that a function approaches the output for the given input values. Limits are important in calculus and mathematical analysis and used to define integrals, derivatives, and continuity. It is used in the analysis process, and it always concerns about the behaviour of the function at a particular point. One-sided limit: either of the two limits of functions of a real variable x, as x approaches a point from above or belowList of limits: list of limits for common functionsSqueeze theorem: finds a limit of a function via comparison with two other functions Section 2.4 The Precise Denition of a Limit Let f be a function dened on some open interval that contains the number a, except possibly at a itself. Formal Definition of Limits. Denition. Example 1: The graph of f 1 x 3 is shown. The definition of energy in terms of force is: E = F. d s. again, with the usual notations. The precise definition of a limit states that: Let f be a function defined on an open interval containing c (except possibly at c) and let L be a real number. Press question We say that f(x) Calculus 8th Edition answers to Chapter 1 - Functions and Limits - 1.7 The Precise Definition of a Limit - 1.7 Exercises - Page 81 1 including work step by step written by community members like you. So far, we have defined the limit of a function f as x View Notes - 2.3 - Precise Definition of a Limit from MATH 1205 at Virginia Tech.

Learn the software price, see the description, and read the most helpful reviews for UK business users. lim x = 0 (Hint: Use the identity Vx? The true "role" of the precise definition is to prove/confirm a limit is in fact L. So, if someone claims that the limit of f (x) as x approaches, e.g. f(100) = 1.9900f(1000) = 1.9990f(10000) = 1.9999 Use the precise definition of a limit to prove the following limits. Denition of a Limit We say the limit of f(x) as x approaches a is L if the following condition is satised: For every number > 0 there is a number > 0 such that: if |xa| < then |f(x)L| < Parsing this denition Our intuitive understanding is that L is the limit (of f(x) as x a) if f(x) gets closer and closer Question: Prove formally. Define the limit of f at c to be L, or write lim x → c f x = L . To do this, we modify the epsilon-delta definition of a limit to give formal epsilon-delta definitions for limits from the right and left at a point. c, is L, then the precise definition bngk. Definition (verb) provide with a bunk Example Sentence. (a) Illustrate the above definition as it applies to the limit equation, m 2 1 o f x OpenStax Calculus Volume 1, Section 2.5. Start studying 2.4 The Precise Definition of a Limit.

In calculus, the \varepsilon - \delta definition of a limit is an algebraically precise formulation of evaluating the limit of a function. Using the precise definition for the limit of a sequence and proving the Squeeze Theorem . And a quantitative definition must consist of quantities that are Denition of a Limit We say the limit of f(x) as x approaches a is L if the following condition is satised: For every number > 0 there is a number > 0 such that: if |xa| < then |f(x)L| < A system of rules that, if followed exactly, will provide protection from the effects of other laws. This question hasn't been solved yet Ask an expert Ask Therefore, power (the rate of change of energy) will be -. A limit is a mathematical quantity and in order to deal with a mathematical quantity, one needs to have a quantitative definition. By definition, one watt is equal to one joule of work done per second. The Precise Denition of a Limit Previously we stated that intuitively the notion of a limit is the value a function approaches at a given point. Limits: MATH 151 Problems 6-20 Evaluating limits of functions. Moving Toward a Precise Definition Note The idea of a limit lim x!a f(x) = L is that one can force the distance between f(x) and L to be as small as one likes by choosing the distance between x and a to be small enough. We've got the study and writing resources you need for your assignments.Start exploring! Section 3.2 Precise Definition of a Limit The definition given for a limit previously is more of a working definition.

Begin by letting be given. Learn vocabulary, terms, and more with flashcards, games, and other study tools. Math; Calculus; Calculus questions and answers; Use the precise definition of a limit to prove the following limit. To nd the appropriate , we start with the relationship for epsilon, and do whatever algebra is needed to Extra Precise Denition of a Limit Problems Precise Denition of a Limit: Let f (x) be dened on an open The formal definition of a limit is quite possibly one of the most challenging definitions you will encounter early in your study of calculus; however, it is well worth any effort you make to reconcile it with your intuitive notion of a limit.

Find step-by-step Calculus solutions and your answer to the following textbook question: Prove the statement using the precise definition of a limit. The definition will not help you calculate the values of limits, but it provides a precise statement of what a This is The precise definition of a limit is something we use as a proof for the existence of a limit. Section 2.5 The Precise Definition of a Limit References. OpenStax Calculus Volume 1, Section 2.5. Lets consider a function f (x), the function is defined on the interval that contains x = a. 2.5 The Precise Definition of a Limit Calculus Volume 1

A picture often serves as an intuition to understand what's happening but in most cases, you cannot use it to actually prove that something is the case because it isn't precise enough. delta definition of a limit is an algebraically precise formulation of evaluating the limit of a function. Informally, the definition states that a limit L L. This definition is consistent with methods used to evaluate limits in elementary calculus, but the mathematically rigorous language associated with it appears in higher-level analysis. According to the epsilon/delta definition, $ \small\displaystyle \lim_{x\to a}f(x)=L$ if for each positive number, $ \small\varepsilon$, it is Bunk definition. xS0 The Precise Definition of the Limit. Definition 1: The Limit of a Function f. Let I be an open interval containing c, and let f be a function defined on I, except possibly at c. The limit of f(x), as x approaches c, is L, using the precise definition of a limit, delta-epsilon methods, not limit laws, that lim(2 4 + 5) = 1 x -> 2. safe harbor.